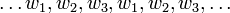Виды фракталов
- Самоподобные множества с необычными свойствами в математике
- Рекурсивная процедура получения фрактальных кривых
- Фракталы как неподвижные точки сжимающих отображений
- Фракталы в комплексной динамике
- Стохастические фракталы
1. Самоподобные множества с необычными свойствами в математике
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:
|
2. Рекурсивная процедура получения фрактальных кривых
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной,подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.
Примерами таких кривых служат:
|
3. Фракталы как неподвижные точки сжимающих отображений
Свойство самоподобия можно математически строго выразить следующим образом. Пусть
Можно показать, что отображение Ψ является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.
Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения |
4. Фракталы в комплексной динамике Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу XX века и связаны с именами Фату и Жюлиа.
Пусть F(z) — многочлен, z0 — комплексное число и рассмотрим следующую последовательность:
Так, множество Жюлиа на картинке справа — множество точек бифуркации для многочлена F(z) = z2 + c, то есть тех значений z0, для которых поведение последовательности zn может резко меняться при сколь угодно малых изменениях z0. Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z) и рассмотрение множества тех значений параметра, при которых последовательность zn демонстрирует определённое поведение при фиксированном z0. Так, множество Мандельброта — это множество всех , при которых zn для F(z) = z2 + c и z0 = 0 не стремится к бесконечности. Ещё один известный пример такого рода — бассейны Ньютона. Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления zn к бесконечности (определяемой, скажем, как наименьший номер n, при котором | zn | превысит фиксированную большую величину A). Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы. |
5.Стохастические фракталы Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов: 
|









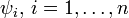 — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:
— сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости: 
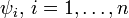 — отображения подобия, а n — число звеньев генератора.
Для треугольника Серпинского n = 3 и отображения ψ1, ψ2, ψ3 — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении Ψ.
В случае, когда отображения ψi — преобразования подобия с коэффициентами ri > 0, размерность s фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения
— отображения подобия, а n — число звеньев генератора.
Для треугольника Серпинского n = 3 и отображения ψ1, ψ2, ψ3 — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении Ψ.
В случае, когда отображения ψi — преобразования подобия с коэффициентами ri > 0, размерность s фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения 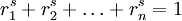 . Так, для треугольника Серпинского получаем s = ln3 / ln2.
По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения Ψ, мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.
. Так, для треугольника Серпинского получаем s = ln3 / ln2.
По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения Ψ, мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.
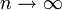 . Эта последовательность может:
. Эта последовательность может: